Implementation of Lattice Quantizer Optimization Using Stochastic Gradient Descent

In this work, we present a Python and C++ implementation that replicates the numerical optimization algorithm for designing lattices with minimal normalized second moments (NSM). The algorithm uses stochastic gradient descent (SGD), treating the NSM as a function of the generator matrix, and updates all elements in the direction of the negative gradient for efficient lattice optimization. We have replicated the algorithm across dimensions from 2 to 16, with a particular focus on 2D and 3D cases, where we provide visualizations of the optimized lattices. Additionally, we apply the theta image representation to all dimensions as a tool for examining the lattice structures. Our results validate the correctness of the original paper’s findings. Our code is publicly available at our GitHub Page.

This work is a team project. I would like to thank my teammates An Ruibo, Xu Yue and Zhang Lingxin.

Problem Definition

Given a n-dimensional continuous space, how to quantize the vectors within with a minimal normalized error? We replicate a method that regards the normalized error as a function of the generator matrix selected, and use gradient descent to optimize over it.

Results

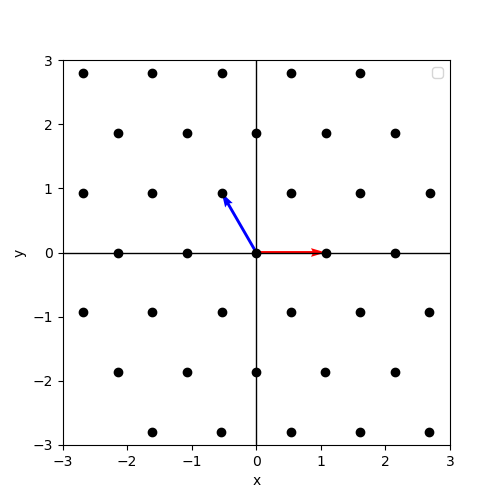
The ground truth of 2d case should be a hexagonal lattice. The ground truth of 3d case should be a face-centered cubic lattice. Our visulization results shown below are consistent with the ground truth.

2d hexagonal lattice

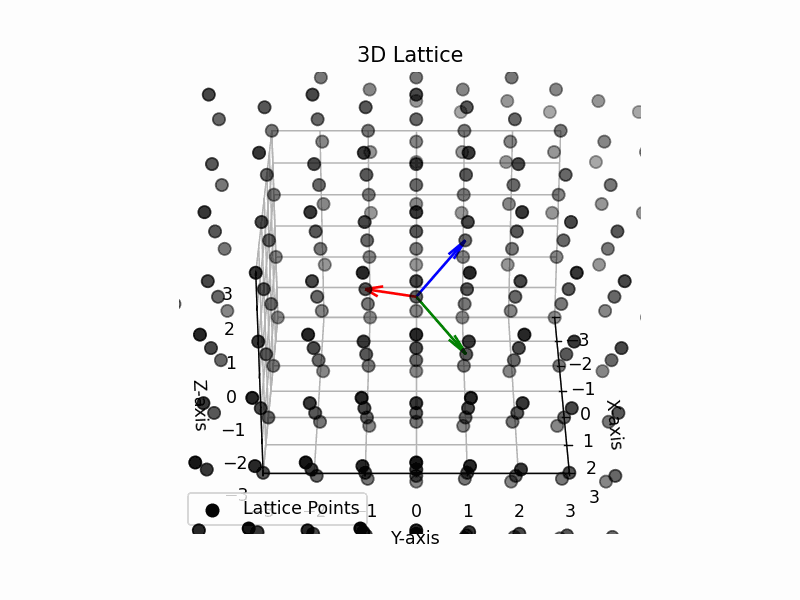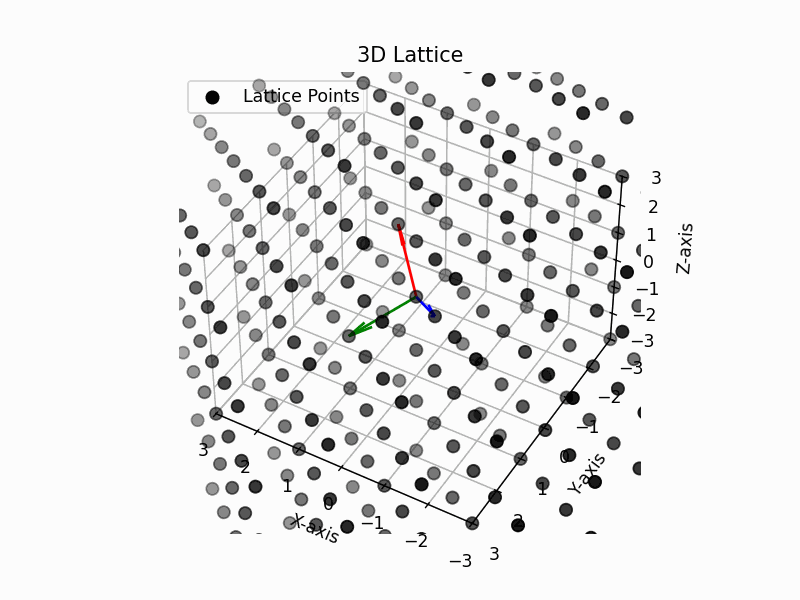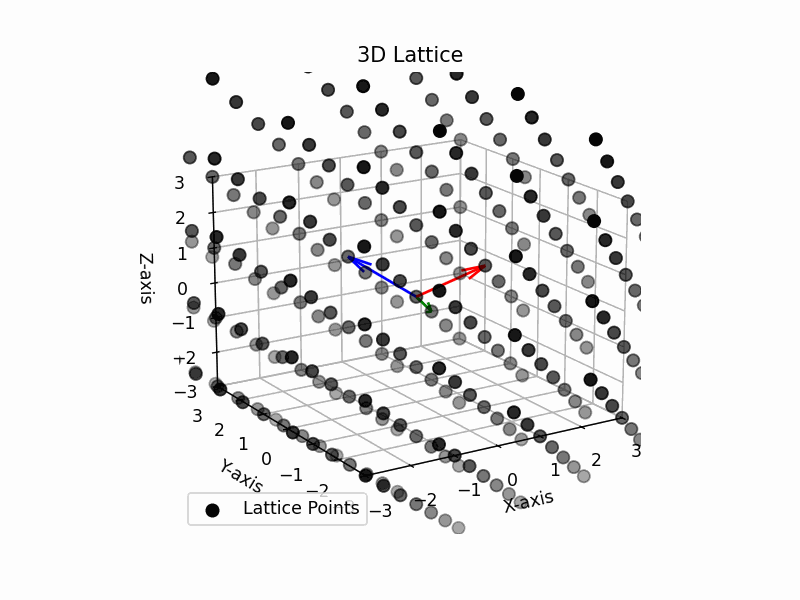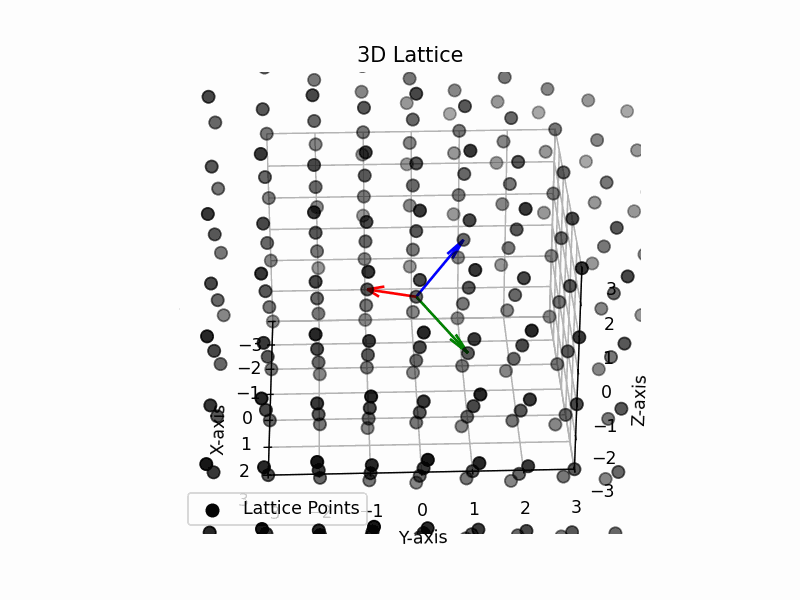3d face-centered cubic lattice

For more results, please refer to our github page.